MLE vs MAP 의 직관적 이해

MLE(Maximum Likelihood Estimation)과 MAP(Maximum A Posteriror estimation)의 차이를 직관적으로 이해하는 건 꽤나 중요한 것 같다.

---

수식으로보면 다음과 같다.

식1. Likelihood

값을 계산하기 위한 2가지 값(파라미터와 입력값) 이 주어졌을 때, 해당 값이 나올 확률이 얼마나 되는지를 likelihood (가능도) 라고 한다.

이 가능도를 최대화 하는게 MLE 이다.

 

식2.Posteriror

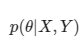
반대로 입력값과 출력값이 주어졌을 때, 해당 파라미터가 나올 확률을 Posterior( 사후확률 ) 이라고 한다.

식3. likelihood x prior

이는 앞에서 본 가능도 x 사전 확률 , 로 나타낼 수 있다.

 

---

이 2가지 방법에서의 관점 차이를 이해하는게 핵심이라고 생각한다.

 

먼저 MLE는 모수가 정해져있다는 가정이 깔려있다.

그렇기에 이 모수 (여기서는 $\theta$ ) 를 찾고 싶은 것이다.

가능도가 최대가 되는 $\theta$ 값을 추정해보자는게 MLE의 목적인 것이다.

 

반대로 MAP는 모수는 계속 변한다는 가정이 깔려있다.

그렇기에 어떤 값이 들어왔을 때 모수 분포를 계속 바꿔나가는 것이다.

 

즉 MLE는 Data가 나올 확률을 최대화하는 것, MAP는 모수가 나올 확률을 최대화하는 것이다.

가정의 차이가 있고 따라서 방법의 차이가 생겨났다고 이해할 수 있겠다.